Can a machine discover the laws of physics by itself—like Newton, but without the apple and without writing the equation by hand?
In June 2025, a new method called H-FEX (Hamiltonian Finite Expression) was published. It doesn’t just predict system behavior—it writes down the math behind it. And crucially, in a form humans can understand.
It’s a form of symbolic learning, increasingly popular over black-box neural networks that work, but don’t tell us why.
🚴 Instead of an apple—an e-scooter on a strange road
Imagine riding a scooter down a weird road with unknown slopes. You speed up, slow down, get pulled or pushed.
Now imagine you have a sensor that records:
- your velocity $ p $,
- your position $ q $,
- and your energy $ H $.
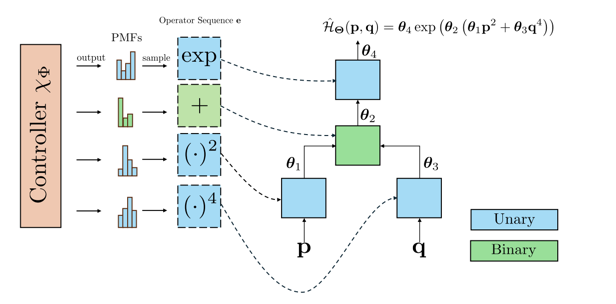
From just these numbers, without knowing the terrain, H-FEX can reconstruct the equation for $ H(p, q) $—a kind of hidden map of your ride.
🧮 Math without black boxes
Many physical systems are described by Hamiltonians—functions like:
$$ H(p, q) = \exp(-p^2 - 1.1q^4) $$
H-FEX finds that equation from scratch, by testing thousands of symbolic expressions and picking the best fit.
📈 How do we know we got it?
If the mean squared error (MSE) is near zero, we know we found a great match. That’s our physical law, rediscovered.
📊 Practical Comparisons: H‑FEX vs SINDy and Others
In Section 4 (“Numerical Results”) of the original paper, the authors present a clear comparison between H‑FEX and other approaches. They evaluate two classic systems — a non-separable Hamiltonian and the three-body problem — and test how well different methods model trajectories and preserve physical laws.
Non-separable Hamiltonian $H(p,q) = \exp(-\alpha_1 p^2 - \alpha_2 q^4)$:
H‑FEX successfully recovered the exact form $\exp(-1.0003,p^2 - 1.1002,q^4)$, nearly identical to the true equation. In long-term simulations (up to 60 time units), it maintained very low trajectory errors and minimal energy drift, unlike SINDy, which gradually diverged from the true dynamics over time.Three-body problem: Thanks to custom-designed interaction nodes, H‑FEX was able to capture the gravitational interactions between three masses better than alternative methods such as HNN, SRNN, or SANN. The resulting trajectories were more accurate and preserved energy more consistently.
These experiments show that H‑FEX not only generates correct symbolic formulas, but also outperforms both symbolic and neural-network-based methods in predictive quality and physical stability.
🔬 Who cares?
- Scientists: rediscover equations from raw data
- Engineers: build better models of machines
- AI folks: get interpretable models, not black boxes
🧠 What about neural networks?
HNNs learn $ H(p, q) $ too—but as a neural function. H-FEX gives you a clear symbolic expression instead. For science, that matters.
✨ Summary
Symbolic methods like H-FEX are machines that write their own equations—and explain them to humans.
📎 Links
- Based on the publication 📄 arXiv:2506.20607 PDF