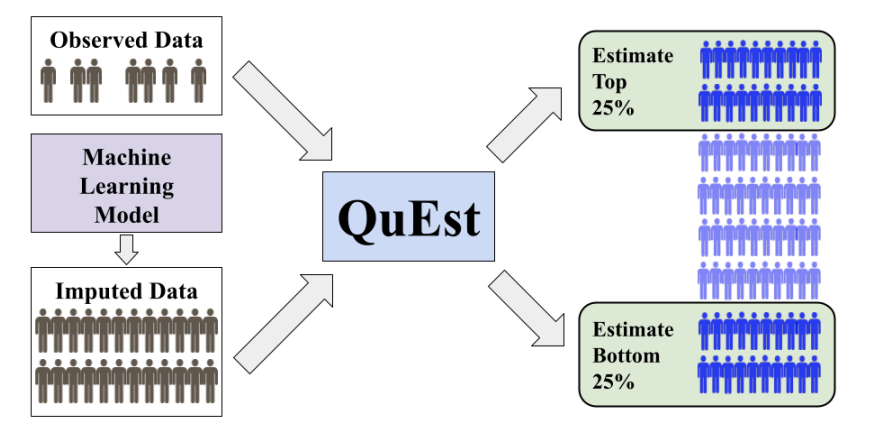
Imagine you track your morning commute times by recording 50 real-world trips with your GPS-enabled phone. You also run a traffic simulator to generate 5,000 possible commute scenarios. You want a reliable estimate of the 95th percentile of commute time—the duration you won’t exceed 95% of the days. Using only your 50 recorded trips yields a wide confidence interval. Using only the simulator risks systematic biases: it might ignore sudden road closures or special events.
QuEst (Quantile-based Estimation) smartly combines both sources:
- It computes the 95th percentile on the real data and on the simulated data.
- It subtracts the simulator’s estimate on just those 50 simulation runs, canceling out any systematic offset.
- It mixes the two estimates with a weight $\lambda$, chosen to minimize the overall sampling variance.
The result is an unbiased, precise estimate of the 95th percentile commute time, with a narrower confidence band than using either source alone.
What Is the QuEst Method?
QuEst estimates any quantile-based measure $Q_\psi(F) = \int_0^1 \psi(p) F^{-1}(p),dp$, where $\psi$ is a weight function (e.g., a delta for a single percentile, or a step for CVaR). It leverages:
- A small set of gold-standard observations ($n$ samples, empirical CDF $F_n$).
- A large set of model-generated imputations ($N$ samples, empirical CDF $\widehat F^e_N$).
The QuEst estimator is enumerator: $$ \widehat Q_\psi(\lambda) = \lambda,Q_\psi(\widehat F^e_N) + \bigl(Q_\psi(F_n) - \lambda,Q_\psi(F^e_n)\bigr), $$ where $F^e_n$ is the simulator’s CDF on the gold sample. This form ensures unbiasedness even if the simulator is biased.
Why Does It Work and Avoid Bias?
- Bias cancellation: Subtracting the simulator’s estimate on the same sample removes any constant offset.
- Optimal weight: The weight $ \lambda^* $ minimizes asymptotic variance: $$ \lambda^* = \frac{\mathrm{Cov}\bigl(Q_\psi(F_n), Q_\psi(F^e_n)\bigr)}{(1 + n/N),\mathrm{Var}\bigl(Q_\psi(\widehat F^e_N)\bigr)}. $$ Empirically, if simulator outputs poorly correlate with real data, $\lambda^*\to 0$, and QuEst defaults to the gold data estimate.
How Does QuEst Self-Correct?
- It estimates variances and covariances from data to choose $\lambda$.
- In an extended version, it parametrizes the weight function $\psi$ as a combination of basis functions and solves a convex optimization to further reduce variance.
- When new real observations arrive, it updates variance estimates, re-computes $\lambda$, and adjusts itself online.
Practical Example: Estimating the 90th Percentile of Website Load Time
Let’s walk through a concrete numeric example using QuEst formulas. Suppose:
- You collect $n=100$ real measurements of page load time, yielding a 90th percentile estimate $Q(F_n)=2.5$ and sample variance 0.04.
- You generate $N=10000$ model-based imputations, giving $Q(\widehat F^e_N)=2.3$ and variance 0.01.
- On the same 100-sample subset of imputations, you compute $Q(F^e_n)=2.4$.
- The covariance between the two estimates is 0.02.
Compute optimal weight $\lambda^*$: $$ \lambda^* = \frac{0.02}{(1 + 100/10000) \times 0.01} \approx 1.98. $$ In practice, cap $ \lambda^* $ at 1, so $ \lambda^*=1 $.
Form the QuEst estimator: $$ \widehat Q_{0.9}(\lambda) = \lambda \times 2.3 + (2.5 - \lambda \times 2.4) = 2.3 + 0.1 = 2.4. $$
Interpretation:
- Pure data-only estimate: 2.5 s (high variance).
- Pure-model estimate: 2.3 s (potential bias).
- QuEst combined estimate: 2.4 s (bias canceled, variance minimized).
This numeric example shows how to plug observed quantiles, variances, and covariances into QuEst’s formulas to obtain a corrected, low-variance estimate.
📎 Links
- Based on the publication 📄 2507.05220