Maszyna, która odkrywa prawa fizyki. Jak działa H‑FEX i co z tego dla nas?

Czy maszyna może samodzielnie odkryć prawo fizyczne — tak jak Newton, ale bez jabłka i bez równania na kartce?

W czerwcu 2025 opublikowano nową pracę opisującą metodę o nazwie H‑FEX (Hamiltonian Finite Expression), która to właśnie robi. Nie tylko przewiduje zachowanie systemu, ale sama tworzy matematyczny wzór, który opisuje jego dynamikę. Co ważne: wzór, który rozumie człowiek.

To przykład tzw. symbolicznego uczenia się, które coraz częściej konkuruje z czarnymi skrzynkami — sieciami neuronowymi, które działają, ale nie dają nam odpowiedzi na pytanie “dlaczego?”.

🚴 Zamiast jabłka — hulajnoga na dziwnej drodze

Wyobraź sobie, że jedziesz hulajnogą po trasie, która nie ma równych nachyleń ani stałych zasad. Tu zjazd, tam podjazd, w jednym miejscu przyciąga Cię bardziej, w innym wypycha. Prędkość $p$ i pozycja $q$ zmieniają się w czasie.

A teraz wyobraź sobie, że masz czujnik, który co chwilę zapisuje:

• Twoją prędkość $p$,
• pozycję $q$,
• i ile energii $H$ miałeś w danym momencie.

Na podstawie samych tych danych, bez znajomości drogi, można odzyskać wzór na $H(p,q)$ — czyli coś w rodzaju mapy tej drogi.

🧮 Matematyka bez czarnej skrzynki

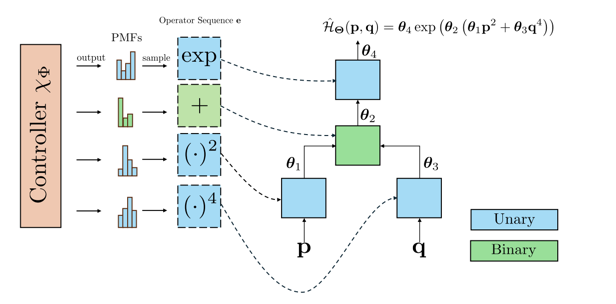
Systemy fizyczne często opisuje się przez tzw. Hamiltoniany – funkcje $H(p,q)$, które mówią, ile energii ma układ w danym stanie.
Przykład:

H‑FEX potrafi odkryć taki wzór od zera, testując dziesiątki tysięcy wyrażeń i wybierając to, które najlepiej pasuje do danych.

📈 I jak wiemy, że trafiliśmy?

Jeśli średni błąd kwadratowy (MSE) ≈ 0, to znaczy, że wzór pasuje do danych — i mamy nasze prawo fizyki.

🔬 Po co to komu?

• dla naukowców — odkrywanie równań z danych,
• dla inżynierów — modelowanie fizyki maszyn,
• dla twórców AI — interpretowalne modele.

📊 Rzeczywiste porównania: H‑FEX vs SINDy i inne

Autorzy w sekcji „Numerical Results” (część 4) prezentują wyraźne porównanie H‑FEX z innymi podejściami. Zbadali dwa klasyczne przypadki – układ nie‑separowalny oraz problem trzech ciał – a następnie oceniali, jak metody radzą sobie z danymi i symulacją trajektorii. Oto, co odkryli:

• Nie-separowalny Hamiltonian $H(p,q)=\exp (-{\alpha }_1{p}^2-{\alpha }_2{q}^4)$:
  H‑FEX dokładnie odzyskała formę $\exp (-1.0003p^2-1.1002q^4)$, co wskazuje na niemal idealne dopasowanie do prawdziwych parametrów. W długoterminowej symulacji (na przedziale czasowym aż do 60 jednostek czasu) uzyskała bardzo niski błąd trajektorii i niemal zerowy drift energii – w odróżnieniu od metody SINDy, która z czasem traciła dokładność i zaczynała dryfować energetycznie.

• Problem trzech ciał: dzięki zastosowaniu specjalnych „węzłów interakcyjnych” H‑FEX lepiej odwzorowywała siły grawitacyjne między trzema masami niż konkurencyjne metody takie jak HNN, SRNN czy SANN. Rezultatem były bardziej precyzyjne trajektorie i lepsze zachowanie energii.

Z tych eksperymentów wynika, że H‑FEX nie tylko generuje prawidłowe matematyczne wzory, ale również daje lepsze wyniki predykcyjne i stabilność energetyczną niż inne podejścia symboliczne lub oparte na sieciach neuronowych.

🧠 A co z sieciami neuronowymi?

Sieci HNN uczą się $H(p,q)$, ale jako funkcję neuronową (czarna skrzynka). H‑FEX zwraca jawny wzór. To ogromna różnica dla nauki.

✨ Podsumowanie

Symboliczne metody jak H‑FEX to maszyny, które same tworzą równania — i potrafią je wyjaśnić człowiekowi.

📎 Linki

• Na podstawie publikacji 📄 arXiv:2506.20607 PDF