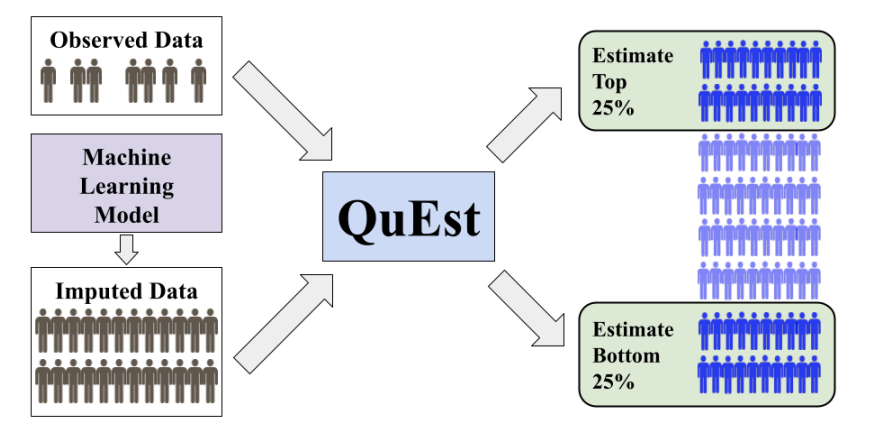
Wyobraź sobie, że rejestrujesz czas swojego porannego dojazdu, wykonując 50 pomiarów GPS. Uruchamiasz też symulator ruchu drogowego, generując 5 000 scenariuszy. Chcesz oszacować 95-ty percentyl czasu dojazdu — czas, którego nie przekroczysz w 95% dni. Korzystając tylko z 50 pomiarów, masz szeroki przedział ufności. Symulator może natomiast systematycznie zaniżać czas (nie uwzględnia korków czy zamknięć dróg).
QuEst sprytnie łączy oba źródła:
- Oblicza 95-ty percentyl na danych rzeczywistych i na symulacjach.
- Odejmuje wynik symulatora obliczony na tych samych 50 symulacjach, znosząc przesunięcie.
- Miesza dwie estymaty wagą $\lambda$, dobraną tak, by zminimalizować wariancję.
Daje to nieobciążony, precyzyjny wynik i węższy przedział ufności niż przy użyciu tylko jednego źródła.
Czym jest metoda QuEst?
QuEst estymuje dowolną miarę opartą na kwantylach $$ Q_\psi(F) = \int_0^1 \psi(p) F^{-1}(p) ,dp, $$ gdzie $\psi$ to funkcja wagowa (np. delta dla pojedynczego kwantyla lub krok dla CVaR). Wykorzystuje:
- Małą próbkę wiarygodnych pomiarów ($n$, empiryczna dystrybuanta $F_n$).
- Dużą próbkę imputacji z modelu ($N$, empiryczna dystrybuanta $\widehat F^e_N$).
Estymator QuEst to $$ \widehat Q_\psi(\lambda) = \lambda,Q_\psi(\widehat F^e_N) + \bigl(Q_\psi(F_n) - \lambda,Q_\psi(F^e_n)\bigr), $$ gdzie $F^e_n$ to dystrybuanta symulacji w próbce. Taka forma gwarantuje nieobciążoność nawet przy błędnym modelu.
Dlaczego działa i nie wprowadza biasu?
- Korekta biasu: Odejście estymaty symulatora od tej samej próby usuwa stałe przesunięcie.
- Optymalna waga: Waga $ \lambda^* $ minimalizuje wariancję: $$ \lambda^* = \frac{\mathrm{Cov}(Q_\psi(F_n), Q_\psi(F^e_n))}{(1 + n/N),\mathrm{Var}(Q_\psi(\widehat F^e_N))}. $$ Jeśli symulacje źle korelują z pomiarami, $\lambda^*\to0$ i QuEst użyje wyłącznie danych rzeczywistych.
Jak QuEst sam się koryguje?
- Szacuje wariancje i kowariancje na podstawie danych, by dobrać $\lambda$.
- W rozszerzeniu parametryzuje wagę $\psi$ i rozwiązuje problem wypukłej optymalizacji dla jeszcze mniejszej wariancji.
- Przy napływie nowych danych realnych aktualizuje oszacowania i adaptuje wagę online.
Szacowanie 90. percentyla czasu ładowania strony
Załóżmy, że mamy następujące dane:
- Zebrano $n=100$ rzeczywistych pomiarów czasu ładowania strony, co daje oszacowanie 90. percentyla $Q(F_n)=2{,}5$ s oraz wariancję próbki $0{,}04$.
- Wygenerowano $N=10000$ imputacji modelowych, co daje $Q(\widehat F^e_N)=2{,}3$ s oraz wariancję $0{,}01$.
- Na tej samej 100-próbkowej podpróbce imputacji obliczono $Q(F^e_n)=2{,}4$ s.
- Kowariancja między dwoma estymatami wynosi $0{,}02$.
Obliczenie optymalnej wagi $\lambda^*$:
$$ \lambda^* = \frac{0{,}02}{\bigl(1 + \tfrac{100}{10000}\bigr)\times 0{,}01} \approx 1{,}98. $$ W praktyce przycinamy $ \lambda^* $ do 1, więc $ \lambda^* = 1 $.Sformułowanie estymatora QuEst:
$$ \widehat Q_{0.9}(\lambda) = \lambda \times 2{,}3 + \bigl(2{,}5 - \lambda \times 2{,}4\bigr) = 2{,}3 + 0{,}1 = 2{,}4. $$Interpretacja:
- Estymat czysto na podstawie danych: 2,5 s (wysoka wariancja).
- Estymat czysto modelowy: 2,3 s (możliwa stronniczość).
- Połączony estymat QuEst: 2,4 s (wyeliminowane przesunięcie, zminimalizowana wariancja).
Ten przykład numeryczny pokazuje, jak w praktyce podstawić obserwowane kwantyle, wariancje i kowariancje do wzorów QuEst, aby uzyskać skorygowane i stabilne estymacje.
📎 Linki
- Na podstawie publikacji 📄 2507.05220